Chapter Six
Millıs Logic as the Basis for
Computer-based Cognitive Aid
December 27, 2011
This
revision has private, previously unpublished, intellectual property of
Paul
Stephen Prueitt, PhD
Abstract:
An interpretation of Quasi
Axiomatic Theory and Millıs logic is made in support of an implementation of
situational logic. Millıs logic[1]
is considered incomplete by most scholars and was never formalized, by Mill, to
the degree that one finds in other areas of mathematical logic, such a fuzzy
logics or rough sets, or the foundations of computing. Quasi Axiomatic
Theory [2]
builds on the originally incomplete Millıs logic and certain interpretations of
the logic formalism of C S Peirce. One way to regard QAT is to think
about an open system of observation where facts are accumulated from direct
experience. Each of these facts is taken as being ³true² because they are
carefully acquired through direct observation of physical reality. The
methodology for QAT is to gather observed facts, and from this set of observed
facts attempt to generate a minimal set of axioms and postulates along with
inference rules that may be used mechanically to assert the observed facts as
well as a set of inferred assertions. The ³self evidence² is derived
through an empirical methodology followed by the use of specific formal
reasoning. Millıs type formal reasoning has five aspects, called ³logical
cannons², by Mill. If this methodology is followed the set of axioms and
postulates, when equipped with that set of inference rules, may be considered a
situational logic. This consideration does force an analysis the nature
of reification of ontological universals from the situational analyses of the
particulars of situations. Particularly as applied to the first three cannons,
a voting procedure is introduced; in this paper and by Prueitt in 1997[3].
This easy computation operationalized the Millıs logic as part of a general
method for developing operational ontology with situational inference. This situational logic might be ³plausibly²
applied to generating conjectured facts that were not observed first hand.
Millıs Logic as the Basis for
Computer-based Cognitive Aid
Paul
Stephen Prueitt, PhD
Table of Contents
Interpretations of Descriptive
Elements
Joint Canon of Agreement and Difference
Objects with Multiple Properties
The Canon of
Concomitant Variation
Part Three:
Situational Language and Bi-level Reasoning
Description of the Minimal Voting Procedure (MVP)
Data Structure for Recording Votes
Data Structure to Record Weighted Votes
Appendix A:
Discrete Homology to Axiomatic Systems
Introduction
The means through which humans instrument cognition is an exciting and
complex area of scholarship. Views
on the nature of cognition and perception arise based on different assumptions
about human nature. However, only
slowly has this scholarship turned to behavioral and cognitive neuroscience and
the many new methods used to study of brain function. The methods supporting empirical investigation heralded by
Francis Bacon, Newtonian and then Mills; may have developed along with a spoken
view regarding the nature of natural law.
This view tacitly asserts that ALL natural phenomena, including the full
spectrum of the natures of living systems, will eventually be explained by a
single coherent theory. This
theory is to be spoken in the language of Hilbert mathematics.
A rigorous formulation of neuroscience has been stimulated by success
from higher mathematics. This
success has been an avenue to explain causation in mechanical systems. Empiricism has hinted at a complete
model of all the processes that support human cognition. The argument is developed well by a
number of scholars, including Sir Roger Penrose[4]
and Ilya Prigogine[5] that this
search for a single coherent theory of everything is misplaced. An understanding of how this search is
in error has taken centuries to frame.
In the time of Newtonian, natural scientists did not know what we know
today. For example, difficult open
questions in mathematics are related to the discretization of dynamics from
models based on ordinary or partial differential equations[6]. These open questions reveal perplexing
difficulties in making full simulations of the processes involved in supporting
human cognition.
Higher mathematics and rigorous logical systems, such as expert
systems, have shown to be limited[7]. Many modern decision support systems
depend on algorithms that are likewise limited. All the way down into modern
materialist science, we see the same success and the same and the same points
of failure. The mathematics of
trajectories defined on a manifold has well-established limitations. This
creates a deep challenge to academic disciplines such as artificial neural
networks[8]. We fail to find closed form solutions,
and thus we turn to numerical simulations. Even here, a number of factors impact our attempt to
simulate all of the brain processes involved in supporting everyday
cognition. A theory of discrete to
continuum homologies is simply incomplete[9]
and does not yet allow logical entailment to be passed back and forth between
simulations of trajectories defined on a manifold. Logical and mechanical
entailments are often aligned, but this alignment has not been found between
the biology involved in human cognition and a formal model of mathematics.
There are things we know about the neuroscience. Mental induction is a cognitive process
acting in a present moment based on certain perceptions and inferences. Mental
induction exists in real time as part of perception. It has a temporal aspect that accounts for fundamental
changes in a non-stationary ³external² ontology; a model of the world. The results of induction include all
natural languages, all well formed belief systems, and all pre-cognitive
feelings experienced by humans. We
do not have a perfect model for any of these phenomena. In comparison to models of stress on
building support-beans in engineering or to models of volumes or probability distributions
we have made only limited advancements in neuro-mathematics.
The problems associated to modeling, or simulating, human cognitive
processes are not fully posed. And
yet the attempt at understanding human thought goes back into our history. The neuroscience will tell us that we
know a great deal about the behavioral neuroscience and the physiology of the
brain system. We understand a
great deal about cellular processes and processes occurring at the level of
chemical proteins in the brain. But we do not have perfect models of cellular or molecular
population interaction using systems of differential equations. Certainly the planar rotator models
have not been successful in modeling logical entailment[10],
see also Appendix A.
Part One:
Simple Enumeration
Aristotle described an inference method called induction by simple
enumeration. The method proposes that: if we have a number of uniform facts and
we do not know of any contrary facts we can make a generalization about these
facts. This type of induction is
³weaker² than a method that would falsify a theory. However, the
induction by simple enumeration may be close to how natural language forms,
through use. It is conjectural on our part to suggest that Aristotle
viewed natural language formation in this way, but we do make the conjecture
that natural language forms in a fashion that involves categorical
processes.
We have the viewpoint that cognitive categories form from an underlying
physics. The physics self
organizes under constraints that are produces of evolution. The nature of evolution is important to
our viewpoint, but for now we must bracket the term and return to a more
complete description later. What
we are looking for is a set of methods that define natural category at two levels
of observation. The first level is
of components seen to be present in more than one instance. The analogy is of chemical atoms like
helium that, at the same time, can be described as a single something, and yet
occurs in greatly distributed locations.
How does the category ³helium² manifest with such regularity?
We wish to achieve a similar regular distribution of category within
algorithmic systems[11]. These components have the nature of
³universals² extracted as a categorical abstraction from the experience of
multiple instances. Their
distribution within a social media[12]
is seen to use a principle called super distribution[13].
Using Quasi Axiomatic Theories (QAT) developed by V. Finn (1991), a set
of "facts" may be placed inside a deductive framework. The
framework may become situationally grounded though perceptual categorization
and induction, producing a reasoning system complete with deductive inference.
However, the validity of such deductive algorithms depends on the validity of a
class of underlying assumptions. In the case of our extension of QAT we make
the assumption that universals, existing as parts of things, are composed to
produce specific instances, which is what we experience. This stratification is
different from Aristotelian assumptions in significant ways.
The Aristotelian assumptions are understood by considering his theory
of causation. The classes of Aristotelian laws:
causation; formal, material, effective and final;
provide examples of induction reasoning about causation
relationships. These laws are deep
and had great utility.
For Aristotle, at least in the interpretation of some, the phenomenon
of cause is related to similarities within a temporal sequence. The
similarity relates elements and may become a model of states of
situations. The similarity between two things can be stated as
< a, r, b >
where r is the relationship. Dis-similarity is provided a
corresponding notation.
At least in how Aristotleıs metaphysics was incorporated into Newtonian
science, these similarities will be crisp in nature. No critical hidden entanglement between similarity classes
is to be tolerated. The world is to be considered as a deterministic
machine. It is this crispness and
absence of entanglements that might be challenged given modern science and
modern understanding of phenomenon like natural language and human
consciousness. There is casual
entanglement. There is also the
absence of a full understanding of the factors involved in human behavior. In fact, it is conjectured that living
systems have hidden causation due to intention and other phenomenon. We
suggest that living system be regarded as open complex systems, and further
suggest that Aristotleıs logic is closed and simple.
Hidden categorical entanglement may be a sufficient reason why
Aristotelian logic does not describe all causation in open complex
systems. Nature is complete with examples of systems that behavior in
non-logical ways. Something may
make a transformation from one category into another category, as in metabolic
activities where a molecular element is given a specific function by a
catalytic process. A number of elements may be brought together and
transformed into a whole that is not the same as the crisp sum of the
parts. In addition to categorical entanglement, we must consider possible
insufficiency in sampling and in description. The measurement of
behaviors of a human being is an example of measurement insufficiency.
The issues themselves become entangled.
Aristotelian logic has assisted us in developing a class of laws of
causation by generalizing from descriptions of many possible cases of
causation. The generalization is
from a specific set of examples and assumes validity to the descriptions of the
examples. However, the choice of examples, and the description of examples in
some type of formal syllogistic language is more problematic than Aristotelian
logic pre-supposes.
" Logic, in
the Middle Ages, and down to the present day in teaching, meant no more than a
scholastic collection of technical terms and rules of syllogistic inference.
Aristotle has spoken, and it was the part of humbler men merely to repeat the
lesson after him. . . . .
The first extension
was the introduction of the inductive method by Bacon and Galileo – by
the former in a theoretical and largely misunderstood form, by the latter in
actual use in establishing the foundations of modern physics and astronomy. ...
But induction, important as it is when regarded as a method of investigation,
does not seem to remain when its work is done: in the final form of a perfected
science, it would seem that everything ought to be deductive. If induction
remains at all, . . . , it remains merely as one of the principles according to
which deductions are effected. Thus the ultimate result of the introduction of
the inductive method seems not the creation of a new kind of non-deductive
reasoning, but rather a widening of the scope of deduction . . ." (Russell (1914))[14]
There is perhaps no real question about the universality of the laws
developed using methods attributed to Aristotle. If the system under observation, for example Galileoıs
observation of the invariants of falling objects, is very stable, then
deductive syllogisms are constructed around that set of laws which govern
physics. However, in open systems, the system has fundamentally changing
internal dynamics. In this case,
the situation is more difficult.
The metaphysics of Aristotle does not have the richness of modern
theories of causation. Even though Aristotelian logic has been applied to a
range of phenomenon, his methods only work if the phenomenon is fully
constrained by known universal law. This is clearly not the case with a class
of phenomenon such as psychological motivation. The constraint from physics is
³still there², always; but perhaps biology sees physics as a partial constraint
and allowing of individual intention.
Part Two: Six Logical Canons
It is may be difficult to explain human inference in terms of the
monotonic / non-monotonic logics fulcrum. This has been the main line of an
approach towards unifying theories of logical entailment and theories of
physical entailment. If we start
from the neuroscience, we see things differently. To establish a different viewpoint is not necessarily the same
as setting aside the history of science, logic or mathematics. We are suggesting that a modified
approach will avoid a limitation that is now quite obvious.
To mention the limitation itself is controversial, and many people have
written on this, so we will not venture in this direction. We appeal directly to common
experience. The notion of truth
from computable algorithms is not very clear. We see in our private experience
that too many open and unresolved concerns exist, and that the results of computed
reasoning is often shallow. Deep
substructure is required for human cognition. A type of deep structure is provided by the architecture
proposed by Prueitt[15].
This architecture has a ³clopen² principle, which is used to open and close the
axiomatic foundation to a formal system.
Opening a formal system is compared with the dissolution of a, physical,
coherent potential field measurable using EEG and other instrumentations.
Mental induction is a cognitive process acting in a present moment
based on certain perceptions and inferences[16].
In scholarship on Tibetan philosophical traditions we find a representation of
Eastern views on perception and inference.
³ In previous
chapters, we have seen that both admit only two forms of instrumental objects,
namely particulars and universals.
Both philosophers take the existence of only two instrumental objects as
the warrant for admitting only two forms of awareness as instrumental:
perception and inference[17].²
The instrumentation of human awareness is defined in various ways. Prueittıs stratification theory places
particulars at one organizational scale and universals at an entirely different
organizational scale. This theory
is consistent with the notion that experience produces abstractions associated
with field potentials and with metabolic processes in the brain system. The metabolic processes may be modeled
as de-coupled planar rotators, and the field potential as the emergent field
manifold as modeled by the Pribram neurowave equations [18]
and by weakly coupled oscillator systems[19]
[20]. The stratification hypothesis by
Prueitt [21] is the
bases for his modification of the use of Millıs logic. Mental induction exists in real
time. Mental induction involves
more than one organizational scale[22]. It has also a temporal aspect that
accounts for fundamental changes in a non-stationary ³external² ontology.
Quasi-axiomatic theories may provide algorithms that are suited for
modeling open systems and thus for modeling the inductive processes involved in
human understanding of open systems.
We say ³may² because the attempt at developing quasi-axiomatic systems;
e.g., systems that allow axiom sets to be replaced, has not been the main focus
of scholarship, research and development.
In our extension of QAT, we see human reasoning as supported
algorithmically through plausible reasoning and periodic updates to axiom
sets. Thus our definition of
quasi-axiomatics is not going to be the same as QAT was in Soviet science. Most important is the possibility that
the axiomatic foundation of an entire system can be regenerated quickly when
results of reasoning provide incorrect results[23].
The father of Soviet QAT is Victor Finn[24]
[25]. His work is based on the work of
Francis Bacon[26] and J. S.
Mill. All three men developed a theory
of causation based on "induction by simple enumeration". At the core
of a common core to these theories is a specific type of similarity analysis.
For Bacon, Mill and Finn similarity defines classes of instances and facts and
conjectures framed within the context of these instances. Mill gave a general
analysis of the existing, mainly Aristotelian, theories of inductive proof and
provided a set of formula and criteria related to the problems of scientific
reasoning. More specifically, Mill formulated five "canons of
reasoning" about casual hypotheses.
As such there is a consistency between Mill and Aristotle.
The central issues we address in our extension of QAT is in the notion
that a single logical system might be found, sufficient to reasoning about any
situation. The issue is the issue
of coherence[27]. We may maintain the consistency in many
approaches to the problem of modeling cognition while at the same time moving
away from the notion that a single reasoning system should be deemed universal in
nature. This focus on real time
interfaces between humans and computing systems is a core part of what we will
propose.
Millıs Canons (1872) may be summarized as follows.
First Canon [Method of
Agreement]: If two or more instances of the phenomenon under investigation have
only one circumstance in common, the circumstance in which alone all the
instances agree is the cause (or effect) of the given phenomenon.
Second Canon [Method
of Difference]: If an instance in which the phenomenon under investigation
occurs, and an instance in which it does not occur, have every circumstance in
common save one, that one occurring only in the former; the circumstance in
which the two instances differ is the effect, or the cause, or an indispensable
part of the cause, of the phenomenon.
Third Canon [Joint
Method of Agreement and Difference]: If two or more instances in which the
phenomenon occurs have only one circumstance in common, while two of more
instances in which it does not occur have nothing in common save the absence of
that circumstance, the circumstance in which the two sets of instances differ
is the effect, or the cause, or an indispensable part of the cause, of the
phenomenon.
Fourth Canon [Method
of Residues]: Subduct from any phenomenon such part as is known by previous
inductions to be the effect of certain antecedents, and the residue of the
phenomenon is the effect of the remaining antecedents. There is a possible
matching between everything not explained and that part of our understanding
that is not explaining anything.
Fifth Canon [Method of
Concomitant Variations]: Whatever phenomenon varies in any manner whenever
another phenomenon varies in some particular manner, is either a cause or an
effect of that phenomenon, or is connected with it through some fact of
causation. This canon is similar
to the use of dependant and independent factors in statistical studies.
Millıs motivation was to formalize a theory of inferential inductive
knowledge based on the concept of natural law. For Mill, natural law referred
to relationships between antecedent and consequent events that are universally
invariant. The validity of the
inductive generalization was grounded in the invariance of these natural laws.
As we will see, this is a point of disagreement between Mill and Peirce. The
disagreement is in essence about whether or not there is a unique nature to
each perception in real time.
In the Peircean sense, the interpretant makes a judgment about a set of
signs, and in this way imparts something that is not in the signs at all. We interpret this point to build
situational logics that are bi-level and thus separated except during a
meta-phenomenon of emergence. The
Peircean notion of, human interpretant might be more fully supported, and is
recognized to have something essential that the computed reasoning system
cannot have, due to the nature of computing system and the nature of natural
(non-computed) systems. Perhaps
this was the direction the Finn took, perhaps not. However, my work is intending to create a real time
interface through which a human interpretation of formal results might
immediately have an impact on the state of computed reasoning.
We take a "Peircean interpretation" of the canons by making
two changes in philosophy. First, the ³cause² we are looking for is a
"compositional cause" where basic elements are composed into emergent
wholes. Pierce used the metaphor of chemical compounds having been composed by
atoms. The set of compositional causes of chemical properties is then ascribed as
the presence or absence of specific atoms in the chemical composition. However, if the full set of laws of
chemistry are not known, we have a method for discovering the laws of
chemistry. Further, if the full
set of laws of human behavior is not fully discovered, we may have a method
that makes some contribution to our understanding of human behavior. Whether or not there is a full set of
laws is left open.
Second, the invariance that we look for are situational invariants that
are defined across basins of similarity within specific organizational
contexts. The issue of context is perhaps best seen in the application of
Millıs logic to text understanding.
All of the canons have a common feature: there are descriptions of
an occurrence of some phenomenon under investigation and there are related
descriptions in which the phenomenon does not occur. We take is a necessary reminder that the description
may be incorrectly stated, or that the absence of a specific description may be
a consequence of a measurement problem.
Based on formal means, conclusions are drawn regarding the causes of
phenomenon in situational context.
The starting situation assumes that propositions of the following form
are given.
"p is an observed property of object
O".
The proposition is taken as an empirical observation. Finn, in his 1991
paper, would write this as
p Þ1 O²
The logically connective Þ1 is different from Þ2 in that the first connective means reliable inference
where as the second connective is a plausible inference. When objects have more than one
property, and/or have the possibility of having more than one property; then
the situation is more complex, but still empirical in nature. This situation is addressed in the last
two of Millıs canons.
The Canon of Agreement
This Canon consists of three variations. All of them begin with the
same starting situation:
a property, p, of a
class of objects { Oj } has been identified and we require evidence
regarding the possible cause, c, of an object having this property.
The Variation for Direct Agreement list all situations in which the property p is present. An
intersection, c, is defined over the descriptions of all situations in this
list
c = Ç Ti
where { Ti } is the collection of representational sets for
description of all objects Oi that are known to have the property
p. In this canon we have implicit
the sense that there are a set of descriptors from which in each case Ti
is a subset. How these descriptors
are found was not addressed in Finnıs 1991 paper. However, a means to create a full set of descriptors is
given in Prueitt (2001) [28]
[29]. The lower case ³c² is overloaded with
an interpretation, and thus the notation is missing a step. The interpreted description c is of the
set of descriptors Ç Ti.
If this intersection exist and is not empty the intersection is added
to a list of meaningful "positive" descriptive components and a
conjecture is made that property p is connected by a plausible relation to the
descriptive intersection element c.
Remember that c is a set of descriptors, perhaps composed in some way so
that the resulting ³sign² which is ³c² is evocative of an understanding about
the relationship between described properties and a category of objects.
If the descriptive
structure c is a part of the description of the object then it is plausible
that the object has property p.
Whereas the analysis is over a class of objects { Oj } that
each have a specific property p, the inference is often about whether a
specific object O, not in{ Oj }, has this property. Because of the Peircean view regarding
the interpretation of signs, we separate the descriptive intersection elements
so that these might be made viewable through the computer user interface. This was likely not the way Finn used
the results from Millıs logical canons, but is the way we now may
consider.
The introduction of category theory behind the class of voting
procedures, invented by Prueitt, requires some motivation. Let
O = {
O1 , O2 , . . . , Om }
be some collection of objects.
Some device is used to compute an "observation" Dr
about the objects. We use the following notation to indicate this:
Dr : Oi --> { t1
, t2 , . . . , tn }
This notation is read "the observation Dr of the object
Oi produces the representational set
{ t1 , t2 , . . . , tn
}"
Let P be the union of all individual object
representational sets Tk
made during the observation of a set of objects, O.
T = È Tk.
This notation will be further developed in the last sections of this
paper. The descriptive
intersection elements are then subsets of T. The
elements of T may be encoded using
innovations that Prueitt has discussed elsewhere, so that voting procedures
instrument each of the logical canons.
Let p be from a list of possible properties of an object O. The lower case, ³c², ³dı, ³d-c²,
etc; is used as above to indicate interpreted descriptive elements, composed
from the elements of T. The elements of T are separated from the set of descriptive elements as
a means to require an interpretant to make a composition, or induction. We assume that the truth of p has been
positively assessed. As was
discussed above, this assessment is stated in the form:
p Þ1 O
Which is read: "it is reliable that object O has property p."
We now interpret the Variation for Direct Agreement using a second logical connective, a partially
defined relationship, Þ2 :
c Þ2 O
This should be read: "it is plausible that a description c is
related to a cause of a property similar to property p and that object O has
this property. However, using some equivalence classes we get the following
statement:
Interpreted
substructure c is a plausible cause of property p being a property of object O.
Again, note that the question of which property is under discussion is
not explicitly stated. The
expression "c Þ2 O " is ³about² a single property, the identity
of which is not part of expression.
A separate data system is required to store information about
properties. In this system, the
distinction between these two logical connectives is taken into account.
So called negative knowledge played an important role on the Soviet
QAT. The Variation for Inverse
Agreement lists all situations where
a property p is absent. An intersection, d, is defined over the description of
all situations in this list
d = Ç Ti
where { Ti } is the collection of representational sets for
description of all objects Oi that are known not to have the
property p. Again note the ³=²
will involve an interpretation and that different interpretations may be made
from exactly the same set Ç Ti.
If an intersection, d, in the descriptionıs representational elements
exist and is not empty then this intersection set is added to a list of
meaningful "negative" descriptive components and a conjecture is made
that property p connected by a plausible relation
d Þ2 ~ O.
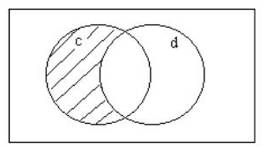
Figure 1:
The representational set c - d.
The descriptive element c – d is then a disqualifier for the
object O have the property under examination.
This is read, " the presence, in O, of the substructure d implies
that the object O does not have the property p".
We could also interpret this to mean:
~ d Þ2 O,
but only under restricted circumstances. It is at this point that we can add various scholarships on
perception and inference. But
again, this is likely never been concerned as part of a bi-level cognitive
aid.
Interpretations
of Descriptive Elements
Let M+p a set of positive examples of objects
having a specific property, p, and M-p be the class of
similar objects that do not have this property.
Note that
~d Þ2 O and c Þ2 O
could imply that
c - d Þ2 O,
where c - d is set c take away the elements of set d. In this case is said to
"block" some of the representational elements in c. Peirceıs notion about the necessity of
interpretation makes a distinction between a subset of the set of all
descriptive elements and the interpreted elements c, d, c – d, ~d,
etc.
The consequences of this are hard to interpret in general. Interpreted elements may be refined,
and may even change over time. A
study of this involves perturbations to the inference engine in the form of
variations in the subsets related to reliable and plausible indicators. This variation does not change the set
of descriptive elements, but does change the set of inferences.
If c is already an intersection of "positive"
representational sets, then the additional removal of some elements may provide
a more minimal concept structure by which to refer to a cause of the property
p. However; in each case, this
possibility must be tested empirically. Finn worked out the means guiding an
empirically grounded testing activity.
For him, the Double Variation of Agreement is exactly a combination of Variation for Direct
Agreement and Variation for
Inverse Agreement. This double
variation is a method for teasing out minimal representations for the measured
indicators of properties of objects.
It seems that two different possibilities exist for the Double
Variation of Agreement. In both
cases, we identify an intersection of a class of examples. One is a class of
negative examples and one is a class of positive examples. In both cases, we
treat the agreement as over a number of examples.
An intersection c, of representational sets, can be the basis of a
conjecture about a positive cause of the property p. Likewise, the intersection d, of representational sets, can
be related a conjecture about a negative cause of the property p. The subsets c
– d (read, "c take away d) (see shaded area in Figure 1) and d
– c can be used in some cases to refine the relationship between causes
and properties. Thus three types of conjectures can be derived with the first
canon.
How the classes of positive and negative examples are selected is
relevant, and this selection criterion is also at the root of similar
variations on the second and third Mill canons.
The Canon of
Difference
For the Canon of Difference
we again obtain descriptions of a class of situations. Certain of the objects
in the situations are described as having property p. For example, again we may
consider the properties as related strongly to the declarative placement of all
objects into one of q categories; e.g., this object has or does not have this
property.
Again, we assume that the description includes a list of
representations about the composition of the objects. These descriptions are
made as logical statements, such as Standard Query Languages (SQL) statements,
that use representational elements from a set T. We may use other retrieval and search standards. The set of interpreted descriptions and
the set of descriptors are encoded as different things, as are sets of possible
properties and encodings of object representations.
As before, let M+p , be a set of positive
examples of an object having a specific property, p, and M-p
be the class of similar objects that does not have this property.
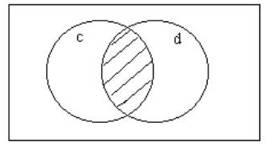
Figure 2:
The intersection between representational sets c and d.
Let Oi be a single element of M+p and
Oj be a single element of M-p. Let c be the
interpreted representational set for Oi and d be the interpreted representational
set for Oj. The intersection can be conjectured to be the
descriptions of how the two objects are "entangled".
If this was the point of an interpretation, the set, c – d, is
the effect, or the cause, or an indispensable part of the cause, of the
property p. It may be that the,
set d – c, is the effect, or the cause, or an indispensable part of the
cause, of a different property q.
The interpretation is what makes the inference. This interpretation is to be stored in
the database. Note that the object
might be a category representational set or even an intersection of some type
derived from the canon of agreement, or from a series of validating steps.
Joint Canon of
Agreement and Difference
The first three of Millıs logical canons were discussed in Francis
Baconıs great work. Francis Bacon is regarded as the father of the scientific
method.
In his magnum opus, Novum Organum, or "new instrument", Francis Bacon argued
that although philosophy at the time mainly used deductive syllogisms to interpret nature, mainly owing to Aristotle's
logic (or Organon), the philosopher should instead proceed through inductive
reasoning from fact to axiom to physical law. (Wiki reference[30])
Again, suppose we have a set of positive examples, M+p,
of objects having a specific property, p, and a set of negative examples , M-p,
when similar objects do not have this property.
We let Cq be the category defined by M+p.
An intersection V+ of the compositional representations of the
positive examples M+p is made. The intersection V-
is defined over the set M-p.
We also look for one example of an object, O, that was not placed into
category Cq while at the same time this objectıs representational
set, d, has an non-empty intersection with M+p.
In the case we have that
V+ Ç d Þ2 ~ O
The same is done with the negative examples to produce the subset of
representations M-. One positive example is chosen and its
representational set, c, used to produce a conjecture about a positive cause.
V- Ç c Þ2 O
The plausible inferences: V+ Ç d Þ2 ~
O and V- Ç c Þ2 O are defined as "dual formal
(positive and negative) causes" of p. The use of such dual statements
produces a distributed assessment of category placement.
Objects
with Multiple Properties
An object O not only has the possibility of having one of several
different properties, but also has the possibility of having multiple
properties at the same time. The first three canons assume that only one
property is being considered. The last two canons treat the more complex
case.
In the general case we may formalize plausible inference regarding a
substructure ai being the reliable cause of a property, pi. In the several advances made by Finn[31],
two logical connectives are linked together, one for plausibility and one for
reliability. The way in which a
judgment on the strength of the inference is varied suggests that degrees of
reliability and plausibility should be developed. This development may be connected to either rough sets[32]
or fuzzy sets[33].
In QAT-like systems, we have three classes of logical atoms; O (objects), P (properties), and A (substructures.)
Substructures are measured with descriptions; T. Certain subsets of descriptions become interpreted
as the elements of substructure.
Only to the degree that it is reasonable to make an assumption of
independence between the causes of properties, we can speak about residues and
concomitant variation. This
principle is noted in several schools of thought as a requirement that certain
types of separation will be measurable in cases where several natural
categories are the object of good measurement.
Suppose we have established k conjectures of the form:
For i = 1, . . . k; pi Þ1 O and ai
Þ2 O.
This maybe read, "For i = 1, . . . k, the property pi
is a reliable property of the object O and substructure ai is the
plausible cause of property pi in object O." Under the
assumption of k independent casual linkages, we can use the compact notation:
(p1 , . . . , pk) Þ1 O and
(a1 , . . . , ak) Þ2 O.
or just,
(a1 , . . . , ak) Þ2 O
in the case that the property set (p1 , . . . , pk)
has already been identified.
In the case where it is necessary to make the relationship between
substructure and property explicit, then we use the notation:
ai Þ2 (O, pi).
This is to read "substructure ai is the plausible cause
of the object O having the property pi². This notation assumes that
pi Þ1 O; e.g., that the object O has property pi is
a reliable inference.
Canon of
Residues
Both the Canon of Residues and the Canon of Concomitant Variation may
deal with complex causes and complex properties.
The first three canons can be used to identify the meaningful subsets
of the set of representational elements T. The last two canons are used, in our interpretation, to further
delineate causal linkages between substructures and properties.
We may set aside some description from any phenomenon such part as is
known by previous inductions to be the effect of certain antecedents. There may be descriptions that do not
account for inferences already taken. The residue of the phenomenon is the
effect of the remaining antecedents.
There is a possible matching between everything not explained and that
part of our understanding that is not explaining anything. This logical canon
assumes that some separation of natural category has already occurred and is
present in our deductive machinery.
We will illustrate.
Let C = { Ci }
be a class of categories of objects. We assume that this class is a reasonably
complete description of the similarity classes of the set of emergent wholes
that are produced by a set of substructural elements (atoms). Again, reflect on the example of the
atomic elements, with its periodic table, and chemistry. The level of
observation of properties chemical compounds might be will separated and
reliable. What is not reliable has
to do with the incomplete measurement of an unknown complex molecule such as a
protein, or the plausible behavior of a society under crisis. The problem addressed by Soviet QAT was
how to make plausible inferences about properties of complex phenomenon such as
exist in nature.
Let A be a generalized
product of some subsets, {a1 , . . . , aq} , of the set A
of substructures:
A = (a1
, . . . , aq)
that are observed to describe a complex set of properties P:
P = {p1
, . . . , pr}
Suppose further that r = q and we know that for each i: i= 1, 2, . . .
, q-1
a1 Þ2
(O, p1),
a2 Þ2
(O, p2),
. . . ,
ar-1 Þ2
(O, pq-1),
It is possible to use the Canon of residues to conjecture that ar
Þ2 (O, pr).
There is a context for this conjecture. The context is the set of
substructures involved in composing objects belonging to one of the categories
in C = { Ci }. These categories in turn are part of a
knowledge base build up to encode knowledge of properties of whole events, or
objects. At present, this type of
system is only approximated, perhaps, by the best of our automated knowledge
management systems.
The Canon of
Concomitant Variation
In this canon we have descriptions of the properties of two objects A
and B. This is a simpler case than
the pervious canon.
Linkages are conjectured. Perhaps the objects are two winter storms A
and B and we are noting that two of the system observables seem to be
proportionately varying. The connection is observed by differences seen in a
common property. The cause of the variation in the property is conjectured to
be though a specific variation in the substructure.
Define a non-specific composition function comp(.) to be a
transformation of some set of substructural elements into a whole that has a
set of properties. We suppose here that the properties are all functional
properties of whole objects. We again suppose that structural-functional
relationships have some degree of independence; i.e., that the functional
properties are distinct and that, at least as a part of the whole, that
distinct structural components are known to compose into distinct properties.
This is expressed:
comp(d + c) ~ comp(d) + comp(c)
where ~ is the connective "is similar to", and d , c are
substructures. Of course, this is a strong assumption that is hedged by the use
of the similarity connective.
Let A and B have a complex of properties:
(p1 , p2 , ., pn-1 ,
comp(c)) Þ1 A
(pn+1 , pn+2 , . . . , pn+m-1
, comp(d)) Þ1 B
and the degree of the presence of substructures c and d is ordered. We
suppose that
c
Þ2 (A, pn,),
and
d
Þ2 (B, pn+m),
where pn = pn+m, is a common property shared by
object A and object B.
Let c+ and d+ denote an increase in c and d
correspondingly and c- and d- denote a decrease of c and
d. Since d is a substructure, d+ and d- maybe defined
either quantitatively or qualitatively (through substructural similarity
analysis.)
Then if the situation:
(p1 , p2 , ., pn-1 ,
comp(c+)) Þ1 A
coincides with the situation:
(pn+1 , pn+2 , . . . , pn+m-1
, comp(d+)) Þ1 B
then we can say that c and d are directly related. A similar
relationship exists when comp(c-) and comp(d-) vary
directly to produce B and A .
In the opposite case, if the situation
(p1 , p2 , ., pn-1 ,
comp(c-)) Þ1 A
coincides with the situation
(pn+2 , pn+3 , . . . , pn+m-1
, comp(d+)) Þ1 B
we say that c and d are inversely related. A similar relationship
exists when comp(c+) and comp(d-) vary inversely.
Clearly, the above notation only begins to define the full set of
possibilities for an algorithmic calculus based on Millıs reasoning. There must
be; however, some finesse in itıs application to complex problems. Millıs logic
breaks down to the degree that the set of observables, both of properties and
substructures, are not composible into independent causal linkages. Moreover,
natural complex systems might not be fully reducible to independent causal
linkages, and a degree of skepticism is required regarding both reductionism
and itıs alternatives. However, as
a practical matter we do find reducibility is a useful assertion.
The problem we see is not the viability of complex descriptions of
bi-level causation, but rather that these descriptions must be situational in
nature. A viable situational form of extensions to Millıs logic might be based
on behavioral evidence that natural systems behave more predictably in
well-defined situational context. In the case that the context has changed, we
may find that the use of certain methods, depending on separation of natural
categories, will fail. This
failure itself is significant that that if methods are well developed we may
use the failure of the system to be a indicator that the system of inference is
out of context. Methods are well
developed then if the system is in context and the results of our algorithms
are producing good matches to observed reality.
Part Three:
Situational Language and Bi-level Reasoning
Using our interpretation of QAT-like formal languages, we conjectured
in 1995, that the J. S. Millıs method creates deductive machinery that is
situational in nature[34].
Acting on this conjecture, we applied a simple form of Millıs logics to
autonomous text understanding[35].
A data repository for storing information provided a framework that did not
depend on specific situations. We
developed a separate formalism that deals only with the "disembodied"
substructure of classes of objects[36]. The methodology built a complete set of
representational symbols for sufficient reference to possible semantics. This framework seems to completely
implement the first three cannons, and to suggest ways in which all of the
canons might be used as a means to study the behavior of complex natural
phenomenon such as human discourse, or the properties of complex proteins.
The representational problem must be treated independently since the
measurement of features, from which substructure is inferred, and properties is
a difficult task in itself. The
representational problem is not solved perfectly by any known algorithmic
system. Our hope is that a certain amount of failure in representational
fidelity might be compensated by adaptation within the framework. This adaptation need not be ³simple²
and might involve the use of evolutionary programs such as artificial neural
networks or genetic algorithms.
But these programs would be sub components within a framework that was essentially
the Millıs logic as appears in Finnıs work in quasi-axiomatics.
In situational logics the interpretation of how logical atom fit
together to form inferences are specific to situational classes. The object of
analysis is assumed to be in a context that maps to one of a known situational
class. When the current situation cannot be mapped to the assumed situational
class, then the logic must be recomputed from an elementary re-measurement of
class and substructure invariants. In this case, either the representational
fidelity or the logical formalism is inadequate. This means that there are two
types of failures to the system we envision. The first is a failure that is easy to fix. The second involves a rather complete
washing out of the old system, and the redevelopment of a new system. The unknown at this point is regarding
what in the architecture remains even in the more difficult case.
The Millıs logic is naturally bi-level, and in this way set a new stage
for logical analysis. Object prototypes are considered as situational classes,
as are modal properties of the environment. Substructural elements are also considered prototypes, but
at a distinct level of organization that is not locally meaningful to the
situational classes of assembled wholes.
A nesting of organizational scales is orchestrated in ways that are
difficult to describe.
Two levels of organization are identified and maintained in separated
data structures. There must be
some ³cross-organizational² scale mechanisms. We have suggested that these are involved in replication of
instances of categories. The
meaningful subsets of representational elements have both internal and external
linkages, the discovery of which leads to one of many possible situational
logics. We interpret the internal linkages to be structural in nature and the
external linkages to be functional in nature.
Structural components are the cause of functional properties that
result from the formation of a whole that is greater than the sum of the
structural components. Water from hydrogen and oxygen is an example. The
compound, water, does not depend on having specific examples of an oxygen atom,
but rather any one of a class of atoms that is the prototype class for all
oxygen atoms.
Extension
of Notation
We will follow and further develop a notation introduced in discussions
of bi-level voting procedures, as seen last two sections of this paper.
However, the objects will be generalized from text passages to generic
objects. Categorization policies are generalized to similarity classes. We are
interested in the property that a "description" is the "formal
cause" of an object being placed into a similarity class. This is clearly
a "synthetic" property that is to be defined by careful empirical
methods and by forming good representations of objects.
The introduction of the category theory behind the class of voting
procedures requires some motivation. Let
O = {
O1 , O2 , . . . , Om }
be some collection of objects.
Some device is used to compute an "observation" Dr
about the objects. We use the following notation to indicate this:
Dr : Oi --> { t1
, t2 , . . . , tn }
This notation is read "the observation Dr of the object
Oi produces the representational set
{ t1 , t2 , . . . , tn
}"
We now combine these object level representations to form a category
representation.
·
each "observation", Dr, of the objects in the training set
O has a representational set
Dr : Oi --> Tk = { t1 , t2 , . . .
, tn }
·
Let P be the union of all
individual object representational sets Tk.
P = È Tk.
This set P is the representation set for the complete collection
O1.
·
The set P can be partitioned, with
overlaps, to match the assignment of objects to categories C = { Cq }. Let T*q be the union of all elements of the representation
sets Tk for all objects
that are assigned to Cq.
T*q = Ç { Tk
| object Ok, is assigned to category Cq. }
In this way, the
category representation set, T*q, is
defined for each category Cq.
The overlap between category representation T*q, and T*s, is one
statistical measure of the "entanglement" between categories Cq
and Cs. This fact leads to a method for identifying the minimal
intersections of descriptions of structural features from the category
representational sets and matching these minimal intersections to logical atoms
in quasi axiomatic theory.
The use of voting procedures to apply the first three cannons is
straightforward, only needing to be tested computationally using some
application such as cyber security or text based security analysis.
On Lattices
We now introduce some additional mathematical constructions that might
be used in QAT-like systems to keep books on the set of all subsets of the
representational elements used in descriptions. These subsets are nodes of the lattice
of subsets with smallest element the empty set and largest element the set of
all representational elements, the universal set, from a class of descriptions.
The notion of minimal meaningful intersections can be seen using a
picture of the lattice. In Figure 3 we see some representational sets and some
subsets. The nodes of the lattice stand for subsets, arranged by the partial
relationship "set inclusion". The nodes form a large diamond shape
with the universal set at the top and the empty set at the bottom.
Note that set inclusion is not a total order since, for example T1
and T2 are not ordered by this relationship. In the figure, the node
m1 could be the intersection of T1 and T2 and
m2 could be the intersection of T1 , T2 and Ti
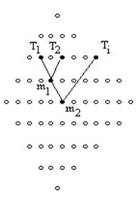
Figure
3: Some substructures and
relationships in the lattice
of
all subsets of the set of all representational elements.
Note that if some manageable set of lattice nodes are identified as
having properties and internode relationships then we have some of the constructions
seen in semantic nets. These constructions have the syntagmatic form < a, r,
b > where a and b are locations and r is a relational property.
It is also worth noting that the size of the lattice is the number 2 to
the power of the size of the universal set. In text understanding systems the
universal set can be many thousands of elements. Thus the lattice is very large
indeed. However all intersections of passage (object) representational sets
will be in a relatively small part of the bottom of the lattice.
Description
of the Minimal Voting Procedure (MVP)
To instantiate a
voting procedure, we need the following triple < C, O1, O2 > :
A set of categories C = { Cq }
as defined by a training set O1.
A means to produce a document
representational set for members of O1.
A means to produce a document
representational set for members of a test set, O2.
We assume that we have
a training collection O1 with m document passages,
O1 = { d1 , d2 , . .
. , dm }
Documents that are not single passages can be substituted here. The
notion introduced above can be generalized to replace documents with a more
abstract notion of an "object".
Objects
O = { O1 , O2 , . . . , Om
}
can be documents, semantic passages that are discontinuously expressed
in the text of documents, or other classes of objects, such as electromagnetic
events, or the coefficients of spectral transforms.
Some representational procedure is used to compute an
"observation" Dr about the semantics of the passages. The
subscript r is used to remind us that various types of observations are
possible and that each of these may result in a different representational set.
For linguistic analysis, each observation produces a set of theme phrases. We
use the following notion to indicate this:
Dr : --> { t1 , t2
, . . . , tn }
This notion is read
"the observation Dr of the passage di produces the
representational set { t1 , t2 , . . . , tn
}"
We now combine these passage level representations to form a category
representation. Each "observation", Dr , of the passages
in the training set O1 has a "set" of theme phrases
Dr : --> Tk = { t1
, t2 , . . . , tn}
Let A be the union of
the individual passage representational sets Tk.
A = Union Tk.
This set A is the
representation set for the complete training collection O1 .
The set A can be partitioned, with overlaps, to match the categories to
which the passages were assigned. Let T*q be the union of all theme
phrase representation sets Tk for all passages that are assigned to
the category q.
T*q = Union Tk such
that, dk, is assigned to the category q.
The category
representation set, T*q, is defined for each category number q.
The overlap between category representation T*q, and T*s,
is one statistical measure of the "cognitive entanglement" between
category q and category s. This fact leads to a method for identifying the
minimal intersections of structural features of the category representational
sets.
J. S. Millıs logics relies on the discovery of meaningful subsets of
representational elements. The first principles of J S Millıs argumentation
are:
1. that negative
evidence should be acquired as well as positive evidence
2. that a bi-level
argumentation should involve a decomposition of passages and categories into a
set of representational phrases
3. that the comparison
of passage and category representation should generalize (provide the grounding
for computational induction) from the training set to the test set .
It is assumed that each "observation", Dk, of the
test set O2 is composed from a "set" of basic elements, in
this case the theme phrases in A. Subsets of the set are composed, or
aggregated, into wholes that are meaningful in a context that depends only
statistically on the characteristics of basic elements.
This general framework
provides for situational reasoning and computational argumentation about
natural systems.
For the time being, it is assumed that the set of basic elements is the
full phrase representational set
A = Union Tk.
for the training
collection O1.
Given the data:
T*q for each C q , q = 1, . . ,
n
and the
representational sets Tk , from the observations Dk, for
each passage, dk, from the test set O2, we generate the
hypothesis that the observation Dk should be categorized into
category q.
This hypothesis will
be voted on by using each phrase in the representational set for Dk
by making the following inquiries for each element ti of the representational
set Tk:
1. does an observation of a passage, Dk,
have the property p, where p is the property that this specific
representational element, ti , is also a member of the representational set T*q for category
q.
2. does an observation of a passage,
Dk, have the property p, where p is the property that this specific
representational element, ti , is not a member of the representational set T*q for
category q.
Truth of the first inquiry produces a positive vote, from the single
passage level representational element, that the passage is in the category.
Truth of the second inquiry produces a negative vote, from the single
representational element, that the passage is not in the category. These votes
are tallied.
Data
Structure for Recording Votes
For each passage, dk , we define the matrix Ak as
a rectangular matrix of size m x h where m is the size of a specific passage
representational set Tk, and h is the number of categories. The
passages are indexed by k, each passage has itıs own matrix.
Each element ti of Tk, will get to vote for or
against the hypothesis that this kth passage should be in the category having
the category representational set T*q. Thus Ak is defined
by the rule:
ai,j = -1 if the phrase is not in T*q
or
ai,j = 1 if the phrase is in T*q
Matrix Ak is used to store the individual + - votes placed
by each agent (i.e., the representational element of the phrase representation
of the passage.)
This linear model produces ties for first place, and places a
semi-order (having ties for places) on the categories by counting discrete
votes for and against the hypothesis that the document is in that category.
Data Structure to Record Weighted Votes
A non-linear
(weighted) model uses internal and external weighting to reduce the probability
of ties to near zero and to account for structural relationships between
themes.
Matrix Bk
is defined:
bi,j = ai,j * weight of the
phrase in Tk
if the phrase is not
in T*q or
bi,j = ai,j * weight of the
phrase in T*q
if the phrase is in T*q
This difference between the two multipliers is necessary and sufficient
to break ties resulting from the linear model (matrix Ak).
For each passage representation and each category, the tally is made
from the matrix Bk and stored in a matrix C having the same number of records
as the size of the document collection, and having h columns – one column
for each category.
The information in matrix C is transformed into a matrix D having the
same dimension as C. The elements of each row in C are reordered by the tally
values. To illustrate, suppose we have only 4 categories and passage 1 tallies
{-1214,-835,451,1242} for categories 1, 2, 3 and 4 respectively. So
cat1 --> -1214, cat2 --> -835, cat3 --> 451
and cat4 --> 1242.
By holding these assignments constant and ordering the elements by size
of tally we have the permutation of the ordering ( 1, 2, 3, 4) to the ordering
(4, 2, 3, 1).
( 1, 2, 3, 4) --> ( 4, 2, 3, 1).
This results show that for passage 1, the first place placement is
category 4, the second place is category 2, etc. The matrix D would then have
(4, 2, 3, 1), as its first row.
Appendix A: Discrete Homology to Axiomatic Systems
Research Note: December 20, 2011
Paul Stephen Prueitt, PhD
Abstract: A formal definition of homology between a set of discrete
state transitions and a trajectory in n-dimensions is discussed in the context
of models of learning in biological systems. Logical and physical entailment might then be
mirrored.
The simplest form for a Lie group[37]
may be seen as an algebraic model of the behavior of a set of linear
transformations, for example as used in modeling visional flow[38]. A Lie group is something that is
simultaneously an algebraic group and a manifold. A good example of a Lie group is a set of matrices defined
as continuous transformation on the points of a vector space. The group properties include a closure
property, and associate property, the existence of an identity element and
inverses.
The concept of a discrete and finite Lie group is a
difficult one and may be seen as ³unnatural². For example, the inverse of an operation that moves a point
s(j) to point s(i) might be equated with a reach ability argument that a composition
of steps starting at s(j) will eventually, in a finite number of steps reach
back to s(i). This requires that
all transition be part of a sequence that returns to previous states. We may require that all state
transitions, { t(k) } be part of a cycle; e.g., if t(k)[s(i)] à s(j), there must exist a finite
sequence of state transactions that compose to bring s(j) back to s(i). However, this may not be enough to
satisfy the definition of an algebraic group.
Such compositions require an associative law. It is not clear how this may be
defined. Closure also requires
some abstraction since for state transition diagrams; state transitions are
defined only on one state.
However, this problem is connected with the vast difference between a
discrete topology[39]
and a topology similar to the topology of open sets in the real line. It is supposed therefore that any
notion of a discrete Lie Group must be defined as a construction having certain
homological properties with a Lie Group defined on a non-discrete space, in
which the discrete space is embedded.
It is this notion of a ³matching² between a finite state transition
diagram and a Lie group that we are concerned with.
For our purposes here, it is proper to consider only those
transformations that take a location within an n- dimension manifold to a,
possibly, different location in the same manifold. The manifold may be defined by a set of first order ordinary
differential equations. A general
question arises, might a discrete group be defined that encodes any finite
state transition diagram, including quasi-axiomatic logics[40];
e.g., as in a Millıs logical cannon derived logical entailment systems[41]. This problem is not fully
resolved. The current paper is
designed to identify areas where incomplete formal work exists.
The question of homology; e.g., reliable mapping between
logical and physical entailments, is then a question of mapping physical
entailments to logical entailment, and visa versa. In logical systems we may see the single step logic as
single steps along a path, or trajectory, created by the transformations from n
dimensions to n dimensions. These
discrete logical paths; e.g., logical entailment, are generally defined using a
transition state rule; e.g.,
(1, 0 , 1 0) à (0, 0, 0, 1) à (1, 1, 1, 1),
Both logical rules and the dynamical rules have domain and
range as subsets of the n-dimensional manifold. If we consider the abstract properties of transition state
diagrams we may find that these diagrams encode all necessary dynamic
entailment necessary to define models of biological functions. However, the central question is
regarding if an arbitrary finite state diagram may be extended to a finite
state diagram having sufficient properties to be embedded as a homology to a
class of simple Lie Algebras.
This question is not closed.
One such example is the set of generalized immunological
response transition diagrams[42]. The transition diagrams in Eisenfeld
and Prueitt (1988) shows a complete discrete model of high and low zone tolerance
response behaviors characterizing any immunological response to novel or
recognized antigens. A system of
piece wise defined first order differential equations was shown by Prueitt
(1988) to pass through all appropriate regions of the associated n dimensional
manifold. This was an original
contribution of Prueitt, which is extended in various later papers[43]
[44]
[45]
[46]
[47].
A formal process for encoding axiomatic systems as finite
state transformations having certain algebraic closure and associative rule, is
developed in additional publications[48]
[49]. The basic definitions of a
discrete to continuum homology are defined in Prueittıs PhD thesis (1988)[50]. The idea then, as it is now, is
to create an ability to encode in real time wave interactions any behavior of a
continuum manifold, e.g., one that arises in the presence of a system of first
order differential equations.
Discrete to continuum manifold mapping, as was shown in the case of
generalized immune response in Prueittıs thesis, suggests the possibility of
electro magnetic wave interference patterns to compute a discrete logic
reliably[51]. A computational model might be
developed that provides additional evidence that cognitive processes are
supported by dendrite-to-dendrite interactions in neuronal groups[52].
The homology theory shown in Prueittıs PhD thesis can be
generalized easily to stochastic equations, so that the categorization of
measurement may be discretized.
The discretization is not merely to a logical value but also to a
normally distributed random variable.
A bursting model of neural associative interactions, seen in [53],
and widely known; is then modeled by the input caused movement in the logical
or the continuum space. The
Pribram neuro-wave model[54]
governing field-to-field interactions between communities of neurons is also
present. The control of groups of
neurons by a single parameter is discussed by several of Pribramıs colleagues[55]. Edelman discusses neuronal
group-selection[56]. Field to field processing is the basis
for the contribution made by Pribram; e.g., his theory of holonomic brain
processing.
Incomplete and/or uncertain information is a big deal. The incomplete knowledge of
situation may be input into these homologies with some but not all of the state
values set to zero. The system
should produce an output (consequence of physical entailment) that guesses at a
classification category, as if ³normal² presence of hidden information were
input along with the non zero inputs.
Those guesses that are judged to be correct may be used to modify the
underlying n-dimensional continuum manifold, and thus a utility function may
govern the evolution of a real inference engine. In other work[57],
we will address the question of information that is judged to be first
occurrences of something; e.g., as not conceivable by the cognitive
system. In this case, the overall
biological response is to turn the matter over to an immune systemıs interface
with cognitive and memory systems.